生成AI（トランスフォーマーモデル）の仕組みを探るーその２

A frosty May’s Bounty

© Copyright Mr Ignavy and licensed for reuse under this Creative Commons Licence.

 

前回は、トランスフォーマーモデルの中でもGPTのようなデコーダーモデルの生成・推論過程の動きについてGeminiと対話しながら見ていきました。

自分自身では、今まで理解したつもりでも何かフワフワしていたところがクリアになった気がしていますが、お読みいただいたみなさんはいかがでしょうか？

今回は、AIモデルの学習過程について、詳しく見ていこうと思うのですが、まずは、一般のニューラルネットワークでの学習側の仕組みを確認していきたいと思います。

＃今回は、ChatGPT o3-mini-highとの対話です。

では、始めましょう。

 

---

 

入力層、2つの隠れ層と、出力層からなるニューラルネットワークの例で、トレーニングデータによる学習中では何が行われているのかを詳しく知りたいので、教えてください。

 

ニューラルネットワークのトレーニングは、主に以下のプロセスを通じてパラメータ（重みとバイアス）を最適化し、モデルが与えられたタスクを適切に学習できるようにするものです。ここでは、入力層、2つの隠れ層、出力層から構成されるネットワークを例に、その詳細な流れを説明します。

1. パラメータの初期化

• 重みとバイアスの設定:
  各層のニューロン間の重み（weight）と各ニューロンに付随するバイアス（bias）は、通常ランダムな値（もしくは特定の初期化手法：XavierやHe初期化など）で初期化されます。これにより、対称性が破られ、ネットワークがニューロンごとに異なる特徴を学習できるようになります。

2. フォワードプロパゲーション（順伝播）

• 入力データの供給:
  トレーニングデータの各サンプルが入力層に投入されます。
• 隠れ層の計算:
  各隠れ層では、入力（または前層からの出力）に対して重み付き和（線形結合）を計算し、そこにバイアスを加えた後、活性化関数（ReLU、シグモイド、tanh など）を適用します。
  例えば、1層目の隠れ層では

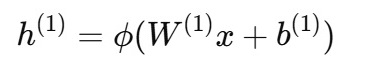
         2層目の隠れ層では、

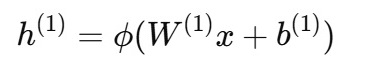
• 出力層の計算:
  最終的に出力層において、隠れ層からの出力に対して同様の計算が行われ、予測値 y^生成されます。タスクに応じて、出力層の活性化関数（回帰の場合は線形、分類の場合はソフトマックスやシグモイドなど）が選ばれます。

3. 損失関数の計算

• 予測と正解の誤差:
  ネットワークの出力 y^と正解ラベル yとの誤差を定量化するため、損失関数（例えば平均二乗誤差、交差エントロピーなど）が計算されます。

         Loss=L(y^,y)

        この損失値は、ネットワーク全体のパフォーマンスを評価する指標となります。

4. バックプロパゲーション（逆伝播）

• 勾配の計算:
  チェーンルールを用いて、損失関数を各パラメータ（重みとバイアス）で微分し、勾配（グラディエント）を計算します。これにより、どのパラメータが損失にどの程度寄与しているかが明らかになります。
  具体的には、出力層から始め、各層に対して誤差を逆伝播させ、

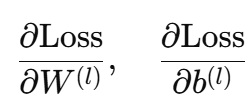
         といった形で各層ごとに計算が進められます。

• 誤差の伝播:
  各層で計算された勾配は、次の層（入力側）に伝播され、各ニューロンでの「責任度」が評価されます。これにより、ネットワーク全体での寄与度が明らかになり、各パラメータの更新方向が決定されます。

5. パラメータの更新

• 最適化アルゴリズムの適用:
  勾配降下法（Gradient Descent）やその改良版（確率的勾配降下法（SGD）、Adam、RMSProp など）を用いて、各パラメータが更新されます。
  更新式の一例（単純なSGDの場合）は以下の通りです。

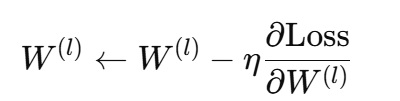
        ここで、ηは学習率を表します。

• 反復更新:
  上記のプロセスは、各エポック（すなわちトレーニングデータ全体を一巡するサイクル）ごとに繰り返され、損失関数が収束するか、あるいは定められたエポック数に達するまで続けられます。

6. 補足：バッチ処理と正則化

• ミニバッチ学習:
  トレーニングデータ全体を一度に使うのではなく、一定数のサンプル（ミニバッチ）に分けて学習することで、計算効率と収束の安定性が向上します。
• 正則化手法:
  過学習（オーバーフィッティング）を防ぐため、L1/L2正則化、ドロップアウト、バッチ正規化などの手法が用いられることがあります。

まとめ

ニューラルネットワークのトレーニング中は、以下の一連のステップが反復的に行われます。

1. フォワードプロパゲーション: 入力データをネットワークに流し込み、各層で線形結合と活性化関数を適用して出力を生成する。
2. 損失関数の計算: 生成された出力と正解データとの誤差を損失関数により定量化する。
3. バックプロパゲーション: 損失の各パラメータに対する勾配をチェーンルールに基づき計算し、誤差を逆方向に伝播する。
4. パラメータ更新: 勾配降下法等の最適化手法により、各層の重みとバイアスを更新する。

このプロセスが繰り返されることで、ニューラルネットワークは徐々にデータの特徴を捉え、最終的には新たな入力データに対しても正確な予測ができるように学習していきます。

 

どうもありがとう。説明内容について確認です。

• 2の隠れ層の計算の説明で、h1、h2が1番目および2番目の隠れ層に渡るデータで、活性化関数をΦ( )のようにあらわしているということですね。
• 4の勾配の計算で「チェーンルール」という言葉が出てきていますが、その説明と、「損失関数を各パラメータで微分すると勾配となる」という点に関して、説明してください。

 

ご確認ありがとうございます。ご指摘の通り、以下の点について確認と補足説明をいたします。

1. 隠れ層の表現について

• h₁, h₂ の意味:
  h₁ は入力層から最初の隠れ層への変換後の出力、h₂ はその h₁ を入力として2番目の隠れ層で計算された出力を表しています。
• 活性化関数 Φ():
  各隠れ層では、線形結合 W^(l)x+b^(l)の結果に対して非線形変換を適用します。この非線形変換は一般的に活性化関数と呼ばれ、ここでは一般記号としてΦ() を用いています。
  例えば、1層目の計算は h₁=Φ(W⁽¹⁾x+b⁽¹⁾)となり、2層目では h₂=Φ(W⁽²⁾h1+b⁽²⁾)という形で表されます。

2. チェーンルールと勾配計算について

        チェーンルール（連鎖律）の基本

• 基本概念:
  チェーンルールは、複合関数の微分を行うための基本的な数学の原理です。
  例えば、2つの関数 fと gに対して、合成関数 h(x)=f(g(x))h(x)の微分は

         h’(x)=f’(g(x))・g’(x)という形で求められます。

      ニューラルネットワークにおける応用

• 層ごとの関数合成:
  ニューラルネットワークでは、入力が複数の層を経由して最終出力に変換されるため、全体は一連の合成関数となっています。例えば、出力 y^が

        y^=Φ⁽³⁾(W⁽³⁾・Φ⁽²⁾(W⁽²⁾・Φ⁽¹⁾(W⁽¹⁾x+b⁽¹⁾)+b⁽²⁾)+b⁽³⁾)

       のように定義されているとき、損失関数 L(y^,y)の各パラメータに対する微分（すなわち勾配）は、         この合成関数に対してチェーンルールを順次適用することで計算されます。

• 具体例:
  例えば、最終層の重み W⁽³⁾に対する損失の微分は、

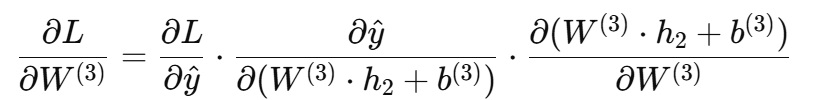
        という風に計算され、ここで各部分は順にチェーンルールを適用して得られます。

勾配（グラディエント）の意味

• 微分と勾配:
  損失関数 Lを各パラメータで微分することで、パラメータの変化が損失に与える影響度を数値的に捉えることができます。この微分値が勾配（グラディエント）です。
• 勾配の役割:
  勾配は、各パラメータの更新方向を示します。具体的には、勾配降下法やその変種を用いて、

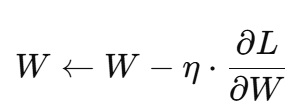
のように、損失が減少する方向にパラメータを更新します。ここで ηは学習率と呼ばれ、更新の大きさを調整するハイパーパラメータです。

まとめ

• 隠れ層の出力:
  h₁と h₂は、それぞれ1層目と2層目の隠れ層で計算された出力であり、各層で活性化関数 Φ()を用いて非線形変換が行われています。
• チェーンルール:
  チェーンルールは、複合関数（ここではニューラルネットワーク全体）の微分を計算するための基礎的な原理であり、各層をまたぐ微分計算において必須です。
• 勾配の計算:
  損失関数を各パラメータで微分することで、そのパラメータに対する勾配が得られ、これによりパラメータ更新の方向と大きさが決定されます。

このような計算がバックプロパゲーションの過程で行われ、ネットワーク全体が徐々に最適なパラメータに収束していきます。

大体わかったのですが、更に実感できるように具体例を用いての説明をお願いします。入力層、2つの隠れ層は2つのノードからなり、出力層は1ノードとして、力層に入る最初のデータは、x₁₁とx₁₂、1番目の隠れ層に入るデータはh₁₁とh₁₂、2番目の隠れ層に入るデータはh₂₁とh₂₂、出力層に渡るデータはy₁、活性化関数をΦ()として、まず、最初のデータが入力層に入って、出力層に渡るまで、次の層のデータがどのように計算されるかを具体的に示してください。

 

• 入力層に渡るデータ： x₁₁ と x₁₂
• 第1隠れ層に渡るデータ： h₁₁ と h₁₂
• 第2隠れ層に渡るデータ： h₂₁ と h₂₂
• 出力層に渡るデータ： y₁
• 活性化関数は Φ()

とし、各層間の重みとバイアスを下記のように表記します。

• _{w1_ij}: 入力層（あるいは隠れ層）から次の層へ接続する重み。ここで、最初の数字が「1」の場合は、接続先が第1隠れ層、「2」の場合は、接続先が第2隠れ層、「3」の場合は接続先が出力層で、2番目の数字「i」は入力側のノード番号、3番目の数字「j」は接続先のノード番号を示します。

1. 入力層 → 第1隠れ層

重みとバイアスの表記：

• 接続は入力層から第1隠れ層なので、重みは w_{1_ij}
  • w_{1_11} は「入力層の1番目のノード x₁₁」から「第1隠れ層の1番目のノード h₁₁」への重み
  • w_{1_21} は「入力層の2番目のノード x₁₂」から「第1隠れ層の1番目のノード h₁₁」への重み
  • w_{1_12} は「入力層の1番目のノード x₁₁」から「第1隠れ層の2番目のノード h₁₂」への重み
  • w_{1_22} は「入力層の2番目のノード x₁₂」から「第1隠れ層の2番目のノード h₁₂」への重み
• バイアスはそれぞれ b_{1_1}（h₁₁ 用）と b_{1_2}（h₁₂ 用）となります。

計算式：

• h₁₁ の計算：

h₁₁=Φ(w_{1_11}⋅x₁₁+w_{1_21}⋅x₁₂+b_{1_1})

• h₁₂ の計算：

h₁₂=Φ(w_{1_12}⋅x₁₁+w_{1_22}⋅x₁₂+b_{1_2})

これにより、入力層の情報 x₁₁,x₁₂ が非線形変換を受け、第1隠れ層の出力 h₁₁,h₁₂となります。

2. 第1隠れ層 → 第2隠れ層

重みとバイアスの表記：

• 接続は第1隠れ層から第2隠れ層なので、重みは w_{2_ij}
  • w_{2_11} は「第1隠れ層の1番目のノード h₁₁」から「第2隠れ層の1番目のノード h₂₁」への重み
  • w_{2_21} は「第1隠れ層の2番目のノード h₁₂」から「第2隠れ層の1番目のノード h₂₁」への重み
  • w_{2_12} は「第1隠れ層の1番目のノード h₁₁」から「第2隠れ層の2番目のノード h₂₂」への重み
  • w_{2_22} は「第1隠れ層の2番目のノード h₁₂」から「第2隠れ層の2番目のノード h₂₂」への重み
• バイアスは b_{2_1}（h₂₁用）と b_{2_2}（h₂₂用）です。

計算式：

• h₂₁の計算：

h₂₁=Φ(w_{2_11}⋅h₁₁+w_{2_21}⋅h₁₂+b_{2_1})

• h₂₂ の計算：

h₂₂=Φ(w_{2_12}⋅h₁₁+w_{2_22}⋅h₁₂+b_{2_2})

この段階で、第1隠れ層の出力 h₁₁、h₁₂ が第2隠れ層へ伝達され、非線形変換を経て h₂₁、h₂₂ が得られます。

3. 第2隠れ層 → 出力層

重みとバイアスの表記：

• 接続は第2隠れ層から出力層なので、重みは w_{3_ij}
  • w_{3_11} は「第2隠れ層の1番目のノード h₂₁」から「出力層のノード y₁」への重み
  • w_{3_21} は「第2隠れ層の2番目のノード h₂₂」から「出力層のード y₁」への重み
• バイアスは b_{3_1}（出力層用）となります。

計算式：

• Y₁ の計算： y₁=Φ(w_{3_11}⋅h₂₁+w_{3_21}⋅h₂₂+b_{3_1})

これにより、第2隠れ層からの情報 h₂₁、h₂₂ が出力層に伝わり、最終的な出力 y₁が得られます。

 

どうもありがとう。ここまでの順伝播の計算の流れを図で整理してみました。

拡大

では、いよいよ、逆伝搬の計算の仕組みに入りたいと思います。損失関数には平均二乗誤差、最適化には勾配下降法を使う場合で、出力層の勾配計算から逆に入力層―隠れ層１間の重みとバイアスの勾配計算について示してください。

以下では、平均二乗誤差 (MSE) を損失関数とし、勾配降下法でパラメータ（重み wおよびバイアス b）を更新する際の「逆伝播（バックプロパゲーション）」の計算手順を、出力層 → 第2隠れ層 → 第1隠れ層 という順序で示します。

なお、活性化関数を Φ(⋅)、その微分を Φ′(⋅)と表記します。また、以下の記号・ネットワーク構成は、これまで順伝播で用いたものと対応しています。

■ ネットワーク構成と記号の整理

層の構成

• 入力層 (2ノード): x₁₁、  x₁₂
• 第1隠れ層 (2ノード): h₁₁=Φ(net_{1_1})、　h₁₂=Φ(net_{1_2})
• 第2隠れ層 (2ノード): h₂₁=Φ(_{net2_1})、　h₂₂=Φ(net_{2_2})
• 出力層 (1ノード): y₁=Φ(net_{3_1})

各層の線形結合（net）の定義

• 第1隠れ層: net_{1_1}=w_{1_11}⋅x₁₁+w_{1_21}⋅x₁₂+b1_1、　net_{1_2}=w_{1_12}⋅x₁₁+w_{1_22}⋅x₁₂+b_{1_2}

• 第2隠れ層: net_{2_1}=w_{2_11}⋅h₁₁+w_{2_21}⋅h₁₂+b_{2_1}、　net_{2_2}=w_{2_12}⋅h₁₁+w_{2_22}⋅h₁₂+b_{2_2}

• 出力層: net_{3_1}=w_{3_11}⋅h₂₁+w_{3_21}⋅h₂₂+b_{3_1}

損失関数 (MSE) の定義

1サンプルあたりの平均二乗誤差を、簡単のため以下の形で定義します（係数の1/2は微分をシンプルにするためにしばしば用いられます）:

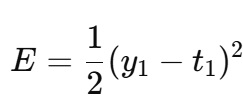
ここで t₁は真の目標値（ラベル）です。

 

1. 出力層の勾配計算

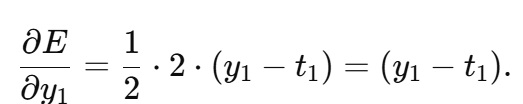
1.1 出力ノードの微分

y1=Φ(net_{3_1})より

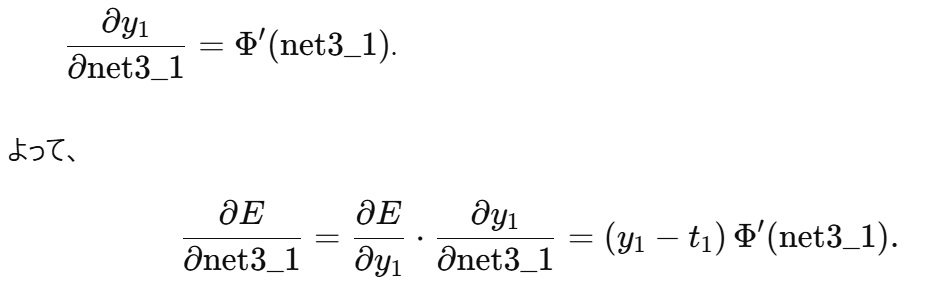
1.2 出力層のパラメータ（重み・バイアス）の勾配

1.3 第2隠れ層出力 h₂₁,h₂₂ の勾配

出力層パラメータを求めた後、次に必要なのは「各隠れ層のノード出力に対する損失の勾配」です。

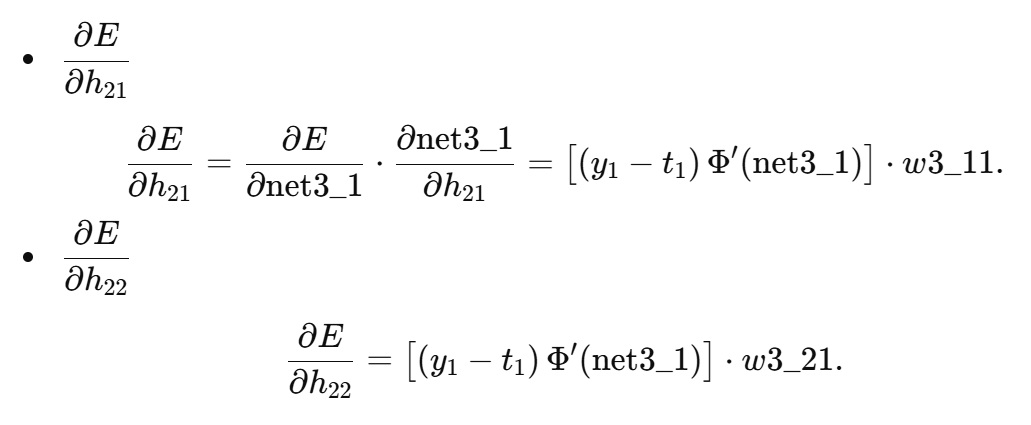
2. 第2隠れ層の勾配計算

2.1 第2隠れ層のノード出力 → net への微分

 

2.2 第2隠れ層パラメータ（重み・バイアス）の勾配

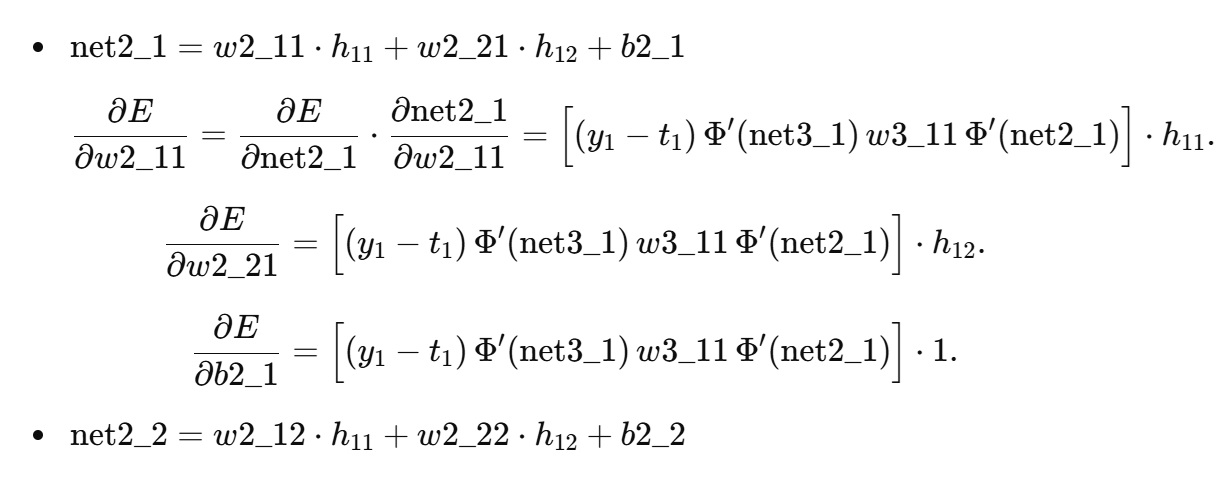
2.3 第1隠れ層出力 h₁₁,h₁₂ の勾配

3. 第1隠れ層の勾配計算

3.1 第1隠れ層のノード出力 → net への微分

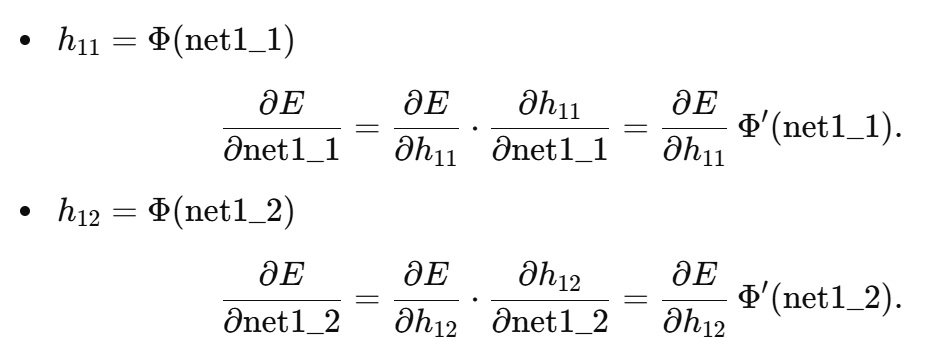
3.2 第1隠れ層パラメータ（重み・バイアス）の勾配

 

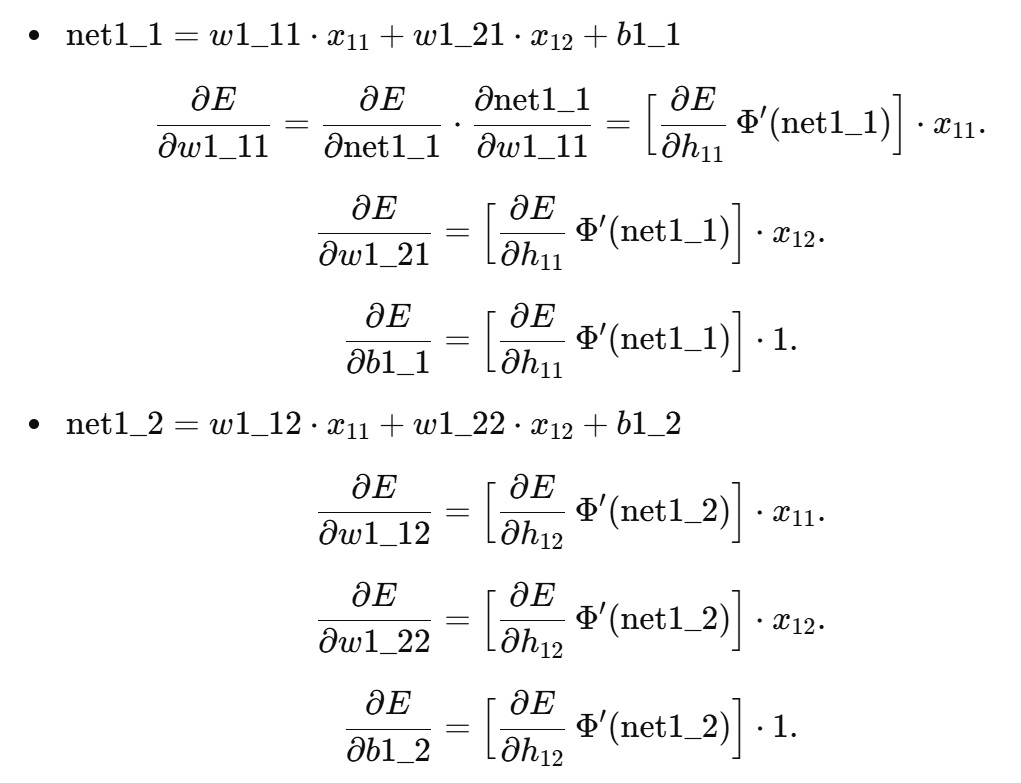
4. まとめと最適化（勾配降下法）

以上のように、出力層 → 第2隠れ層 → 第1隠れ層 へと「誤差」や「勾配」を逆向きに伝播させ、最終的に 各重み・バイアスに対する損失関数の勾配 を求めることができます。

勾配降下法（Gradient Descent）の場合は、求めた勾配を使ってパラメータを以下のように更新します（学習率を η）:

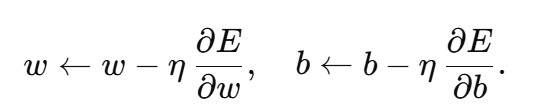
これをトレーニングデータ全体（あるいはミニバッチ）について繰り返し行うことで、損失 E が徐々に減少し、ネットワークは正解値 t₁に近い出力 y₁を生成できるよう学習していきます。

 

勾配計算した結果を使って、今回のニューラルネットワークモデルの15個のパラメータがどのように調整されるか具体的に示してください。

【まとめ：各パラメータの更新式一覧】

1. 出力層
   • w_{3_11}←w_{3_11}−η (y₁−t₁) Φ′(net_{3_1}) h₂₁
   • w_{3_21}←w_{3_21}−η (y₁−t₁) Φ′(net_{3_1}) h₂₂
   • b_{3_1}←b_{3_1}−η (y₁−t₁) Φ′(net_{3_1})
2. 第2隠れ層
   • δ₂₁=(y₁−t₁) Φ′(net_{3_1})  w_{3_11}Φ′(net_{2_1})
   • δ₂₂=(y₁−t₁) Φ′(net_{3_1}) w_{3_21} Φ′(net_{2_2})
   • w_{2_11}←w_{2_11}−η (δ₂₁ h₁₁)
   • w_{2_21}←w_{2_21}−η (δ₂₁ h₁₂)
   • b_{2_1}←b_{2_1}−η δ₂₁
   • w_{2_12}←w_{2_12}−η (δ₂₂ h₁₁)
   • w_{2_22}←w_{2_22}−η (δ₂₂ h₁₂)
   • b_{2_2}←b_{2_2}−η δ₂₂
3. 第1隠れ層
   • δ₁₁=[δ₂₁ w_{2_11}+δ₂₂ w_{2_12}] Φ′(net_{1_1})
   • δ₁₂=[δ₂₁ w_{2_21}+δ₂₂ w_{2_22}] Φ′(net_{1_2})
   • w_{1_11}←w_{1_11}−η (δ₁₁ x₁₁)
   • w_{1_21}←w_{1_21}−η (δ₁₁ x₁₂)
   • b_{1_1}←b_{1_1}−η δ₁₁
   • w_{1_12}←w_{1_12}−η (δ₁₂ x₁₁)
   • w_{1_22}←w_{1_22}−η (δ₁₂ x₁₂)
   • b_{1_2}←b_{1_2}−η δ₁₂

このように、各層で求めた勾配（デルタ項）とその層への入力（前層の出力または元の入力）を掛け合わせ、学習率 η乗じて現在のパラメータから引くことで、各パラメータが調整されます。これが1サンプルに対するバックプロパゲーションの具体的なパラメータ更新の流れです。

 

実際には、重みおよびバイアスの値の更新はミニバッチごとにおこなうということですね。今回の例で行くと、ミニバッチのデータサイズ分、15個のパラメータについて計算した勾配情報を保存しておき、最後に、個々のパラメータについて、計算しておいた勾配の数値の平均をとってから、その平均値を用いてパラメータを調整するという感じでしょうか？

なるほど、学習データにノイズがあっても、ノイズの影響を小さくできるということですね。バッチサイズは多分学習を行わせるコンピュータの処理能力によると思いますが、通常はどの程度一度に学習させるのでしょうか？

そうですね。実際のところ、ミニバッチのサイズはハードウェアのメモリ容量や計算能力、そしてモデルの複雑さやデータの性質に依存します。一般的には、32、64、128、あるいは256程度がよく使われます。

• 小さいサイズ (例：16～32)
  ・メモリに余裕がなく、各サンプルの更新のばらつきを多く取り入れる場合に使われることがあります。
• 中程度 (例：64～128)
  ・多くのタスクでバランスが良く、計算効率と学習の安定性が保たれるとされています。
• 大きいサイズ (例：256以上)
  ・データセットが非常に大きく、またGPUメモリが豊富な場合に使われることがありますが、あまり大きすぎると「局所的な」情報が薄まる可能性もあります。

結局、最適なバッチサイズは実験によって調整されるハイパーパラメータであり、使用する環境やタスクに合わせて決めるのが一般的です。

 

AI学習処理で出てくる「エポック」についても説明してもらえますか？

エポックとは、学習データ全体をモデルに一度すべて通して処理する「1回分の学習サイクル」のことを指します。

• 詳細説明
  • 全データの通過:
    1エポックでは、訓練用の全サンプルが少なくとも一度、順伝播および逆伝播を通じてモデルに入力され、パラメータの更新が行われます。
  • ミニバッチの場合:
    ミニバッチ学習の場合、データセットは小さなグループ（バッチ）に分割されます。各バッチごとにパラメータが更新され、全バッチ分の更新が完了したタイミングが1エポックとなります。
  • 学習の進行:
    エポックを重ねることで、モデルはデータ全体のパターンを反復的に学習し、誤差を徐々に低減させることが期待されます。しかし、エポック数が多すぎると過学習のリスクがあるため、エポック数はハイパーパラメータとして適切に設定する必要があります。

エポックは学習プロセスの進行状況を把握するための指標ともなり、例えば「10エポック後には精度が安定している」「20エポックで収束した」といった形で、学習の効率や収束具合を評価する際に用いられます。

 

同じ学習データを10回も20回も使って学習させる意味があるのでしょうか？

同じ学習データを複数回使う（複数エポックで学習する）理由は、ニューラルネットワークのパラメータは初期状態ではランダムな値から始まるため、各データサンプルから得られる情報を何度も反映させて、損失関数の最小化を段階的に達成する必要があるからです。

例えば、1エポック目ではまだ十分に学習が進んでおらず、パラメータの更新は粗い調整に留まる可能性があります。しかし、データ全体を何度も繰り返し使うことで、以下のようなメリットがあります。

• 段階的な収束:
  各エポックでパラメータが少しずつ最適化され、全体として損失関数が低減していきます。これにより、モデルがデータのパターンや特徴をより正確に学習できるようになります。
• 安定した勾配の推定:
  1回のパスだけではサンプルごとのばらつきが大きい場合もありますが、複数回の更新を通じて、より正確な勾配情報が蓄積され、更新が安定していきます。
• データの多様性の活用:
  学習データが限られている場合、何度も同じデータを用いることで、各サンプルの情報を十分に活用し、モデルの一般化性能を向上させることができます。加えて、エポックごとにデータの順序をシャッフルするなどの手法を取り入れることで、同じデータを使いつつも多様な学習パターンをモデルに学ばせることが可能です。

まとめると、同じデータを10回や20回使って学習させることは、モデルが訓練データに対して徐々に精度を高め、安定して収束するために不可欠なプロセスなのです。

 

『読書百編、意自ずから通ず』と言いますが、AI学習にも通ずるところを感じました。

おっしゃる通りです。「読書百編、意自ずから通ず」という言葉は、たくさんの本に触れることで自然と深い理解が得られるという意味ですが、これはAIの学習プロセスにもよく似ています。AIは同じデータを何度も繰り返し学習することで、各サンプルから得られる情報を統合し、徐々にパラメータを最適化していきます。この反復的な学習が、最初は断片的な情報であっても、次第に全体像を把握できるようにするのです。人間の学びとAIの学習、どちらも「継続は力なり」という点で共通しており、とても興味深いアナロジーだと思います。

 

後、パラメータの調整に関して、今回は勾配下降法での説明をしてもらいましたが、他の方法について簡単に説明してもらえますか？

もちろんです。勾配降下法は基本的な最適化手法ですが、実際の学習ではより高速に、または安定して収束させるためにさまざまな改良手法が用いられます。以下にいくつかの代表的な方法を示します。

1. 確率的勾配降下法（SGD）
   • 基本の勾配降下法と同様の更新式ですが、全データではなくランダムに抽出したミニバッチ（または1サンプル）で勾配を計算します。
   • 更新ごとにノイズが混ざりますが、これが局所的な最適解から脱出するのに役立つ場合もあります。
2. モメンタム付き勾配降下法
   • 過去の勾配情報を「慣性」として加味することで、更新の方向性を滑らかにし、振動を抑えながらより速い収束を狙います。
   • 具体的には、更新に前回までの「速度ベクトル」を加える形でパラメータを調整します。
3. Nesterov加速勾配（Nesterov Accelerated Gradient, NAG）
   • モメンタム法の改良版で、現在のパラメータではなく、予測されたパラメータ位置で勾配を計算する手法です。
   • これにより、更新前に先読みを行い、より精度の高い方向修正が可能になります。
4. AdaGrad
   • 各パラメータごとに個別の学習率を適用する方法で、過去の勾配の二乗和に基づいて学習率を自動調整します。
   • 頻繁に更新されるパラメータの学習率は低く、あまり更新されないパラメータの学習率は高くなるため、疎なデータに対して有効です。
5. RMSProp
   • AdaGradの欠点（学習率が急速に減衰してしまう問題）を克服するため、勾配の二乗和の移動平均を用いて学習率を調整します。
   • 特にリカレントニューラルネットワーク（RNN）など、連続したデータ学習でよく使われます。
6. Adam（Adaptive Moment Estimation）
   • モメンタムとRMSPropの良いところを組み合わせた手法で、勾配の平均（1次モーメント）と二乗平均（2次モーメント）の両方を用いて学習率を調整します。
   • 近年はその収束の速さと安定性から、最も広く用いられる最適化手法のひとつとなっています。

これらの手法は、単純な勾配降下法よりも学習の収束が速かったり、局所最適解に陥りにくかったりするなどの利点があり、タスクやモデルの特性、使用するハードウェア環境に応じて使い分けられています。

長くなってしまったので、今回はここで終わろうと思いますが、次の機会に、トランフォーマーモデルの場合の学習はどのような仕組みなのか教えてもらおうと思います。どうもありがとう。

了解しました。こちらこそ、ありがとうございました。次回、トランスフォーマーモデルの学習について詳しくご説明できるのを楽しみにしております。引き続きよろしくお願いいたします。

---

本日は以上です。

 

終わり